The Quad: An international conference just redefined the kilogram. What does that mean?
By Jack Tulyag
Nov. 27, 2018 5:45 p.m.
The kilogram finally has a precise meaning despite defying a rigorous definition for over a century.
Delegates of the General Conference on Weights and Measures unanimously voted Nov. 16 in favor of a fundamental change in the way we define our basic units of measurement, relying on universal constants of nature rather than previously imprecise definitions. The past definitions either relied on experiments or objects, both of which carried uncertainty to them. The changes, which will take effect May 20, are most notable for the kilogram, Kelvin, ampere and mole.
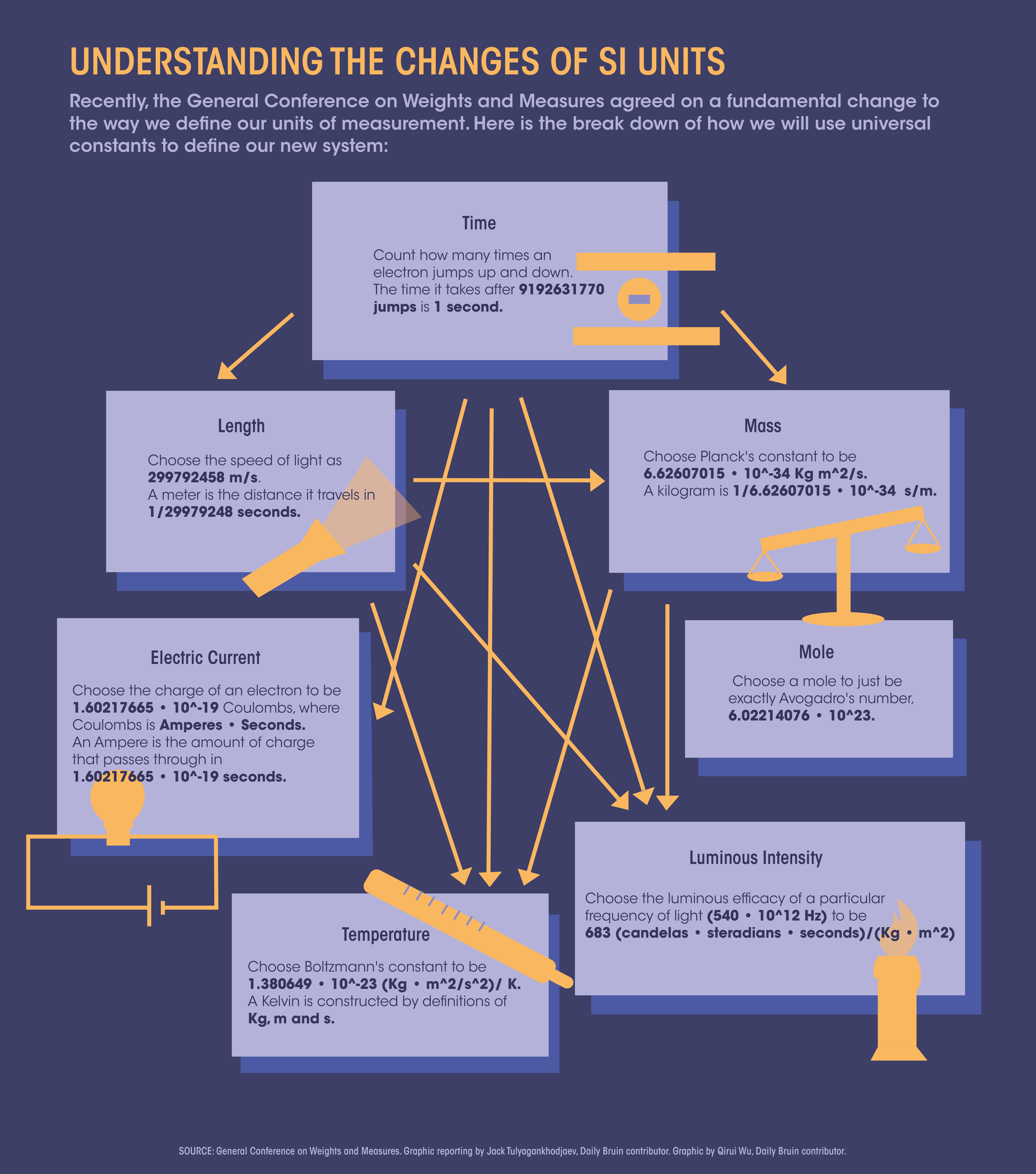
The new definitions reflect a deeper understanding of our universe, instituting a major change to the metric system ever since it was created during the French Revolution. Some of us may have come across this diagram describing the new SI system and found it confusing. We’ll try to explain it.
Base dimensions
The International System of Units (SI) exists to describe physical dimensions. The technical term may seem intimidating, but in reality we think about these all the time. When we ask, “How much time will it take to get to the UCLA Luskin School of Public Affairs?” or “How fast is the rider on that Bird going?” or “How hot is it today?”, we are talking about physical dimensions such as time, speed and temperature
Each question asks about a unit of measurement. Intuitively, a physical dimension is something that can quantitatively describe our world.
It’s natural to incorporate an elegant system to talk about our world, and this is where base units come in.
All units are constructed from a set of more basic units. Some are fundamental in the sense that describing them is more difficult than it’s worth. Some are chosen for convenience of measurement and may have more fundamental aspects to them. Think of them as building blocks that can describe the world around us.
One example is time. Time is a tricky concept to describe scientifically. It’s how long something takes to happen. But that definition implies the reader already knows what time is since they know what it feels like for something to take a long time. Another example is length. It’s how long something is. Even a quick online search doesn’t do much better than this definition.
Now if you put them together, they start to describe interesting things and all it takes is simple multiplication and division. If we ask, “How much distance do I travel in some time?” we understand this to be speed. Mathematically, this means speed is length divided by time.
There are a number of other physical quantities that can be constructed using these base units, especially when we introduce other base units. In total, there are seven: time, length, mass, electric current, temperature, luminosity and number of entities.
Universal constants
While powerful, base units remain useless without any quantitative backing. This is where the concept of universal constants come in to play.
The concept of a universal constant is one of great mystery. These constants are very particular – some have dimensions attached to them, and some are just numbers. As physics has developed from philosopher Isaac Newton’s book “Philosophiae Naturalis Principia Mathematica” to the Standard Model of particle physics, more physical constants have emerged. How can it be, that there are numbers that are so seemingly arbitrary, yet they dictate how our universe runs?
Some physicists suggest that any tiny change to these numbers would have dramatic consequences to the way our universe would work. Take, for example, the number 0.007, something that shows up in nuclear physics and describes how well our protons are glued together. Any smaller and the only element that would exist is hydrogen. Any larger and the only elements that would exist would be the heavy ones such as lead.
Constants with dimensions are relevant to the measuring world. One example is the speed of light, describing the absolute limit to how fast something can travel.
A new era of standardized measurements
Armed with the power of universal constants, we can define what our units of measurement should be. We need only a few: the speed of light, Planck’s constant, Boltzmann’s constant and the elementary charge.
We run into a problem: How do we get the values of our constants if we do not even have definitions of meters or seconds yet?
We measure the value of a constant using experiment. We do it over and over again and in different ways until we determine an accurate number for the constant. The problem is that we are using preconceived notions of meters, seconds and kilograms. Using meter sticks and chunks of metal leads to uncertainty in our constants.
Before the change, kilograms was defined by a particular mass of platinum, amperes relied on two wires carrying current next to each other and the mole was the amount of atoms in 12 grams of carbon-12.
This is a problem because our universal constants should be as exact as possible.
The fix is to turn this on its head. Once we have a pretty good idea of what our number should be using our meter sticks and chunks of metal, we fix the value of a constant to be exact. Then, we use the constants to redefine our dimensions so that all uncertainty sits with our units, not with the universal constant. The role of experimentation is to create consistency among the numbers such that society does not need to reconstruct itself around new values.
We start by defining time. The most reliable thing we can do is count how much an electron jumps up and down within a caesium-133 atom. A second is the amount of time that passes after an electron jumps up and down 9,192,631,770 times. The official definition set by the International Committee for Weights and Measures is the transition between two hyperfine levels of the ground state, but that is essentially the equivalent of saying “jumping.”
If we have time, we may use the speed of light, with dimensions of length divided by time, to define the meter. Once we have a definition of a second, we choose the speed of light to be 299,792,458 meters per second, using this new unit of length called a meter. The length that light travels in one 299,792,458 seconds is one meter.
The same idea goes with choosing the other constants: Planck’s constant, Boltzmann’s constant, the electron charge and Avogadro’s number.
A special note should be made about the Planck’s constant. Despite encountering it in introductory chemistry courses, it’s not at all obvious what it means at first glance since it has dimensions of energy multiplied by time. We can use the power of base units to analyze unusual dimensions such as this. Unraveling it, it can be shown that this is exactly equivalent to angular momentum-a quantity associated with how “heavy” something spins.
The changes dramatically alter the standardization of measurements within the scientific community. Previous definitions carried significant uncertainty, such as the kilogram, defined by a chunk of platinum sitting in a glass jar. The mass was slowly changing over time and proved unreliable.
With such dramatic changes to our system of measurement, it is curious to think about how this changes our daily lives. The answer is that it doesn’t. But that’s the point. Redefinitions of measurement are not intended to change the way we use them. They are intended so that no matter what part of the universe we are in, the definition of meters, seconds, kilograms will be exactly the same, and that there is consistency in our language and experiments.

